Las fracciones se trabajan en el II Ciclo de la Educación Primaria. En cuarto año se introduce el concepto de fracción (se inicia con la interpretación parte-todo). Se trabaja la fracción propia, su escritura, lectura, diferentes representaciones y comparación (>, <, =). En el análisis de fracciones propias es relevante que se utilicen para la comprensión de textos y noticias (MEP, 2012, p.195). Además, gradualmente se debe ir introduciendo otras interpretaciones del concepto de fracción para evitar limitaciones conceptuales mas adelante.
Para quinto año se introducen las fracciones impropias, la representación mixta y la ubicación en la recta numérica. En este nivel continua siendo importante la utilización de problemas contextualizados que permiten un acercamiento natural con las diferentes interpretaciones de la fracción y sus diferentes representaciones.
En sexto año el trabajo se centra en las operaciones con fracciones. Durante este proceso no se debe seguir un enfoque algorítmico, es decir, evitar la enseñanza exclusiva de pasos o procedimientos sin comprender su origen, se deben proponer problemas para que sean resueltos utilizando medios empíricos y/o representaciones y luego formalizar un método para realizar la operación.
En sexto año el trabajo se centra en las operaciones con fracciones. Durante este proceso no se debe seguir un enfoque algorítmico, es decir, evitar la enseñanza exclusiva de pasos o procedimientos sin comprender su origen, se deben proponer problemas para que sean resueltos utilizando medios empíricos y/o representaciones y luego formalizar un método para realizar la operación.
Sobre las habilidades específicas y conocimientos
Los conocimientos previos son fundamentales para poder trabajar algunas habilidades específicas de octavo año en el área de Números, por está razón, esta Unidad Virtual de Aprendizaje (UVA) sirve de enlace entre lo trabajado en Primaria y lo que se trabajará en la Educación Secundaria.
Con el problema ¿Cuánto comprar? , se trabajan las siguientes habilidades específicas de sexto año:
- Simplificar y amplificar fracciones (MEP, 2012, p.189)
- Multiplicar y dividir fracciones (MEP, 2012, p.189)
- Sumar y restar fracciones homogéneas y heterogéneas (MEP, 2012, p.189)
El estudiantado posee conocimientos previos básicos y ha trabajado las siguientes habilidades específicas relacionadas con el tema en quinto año que son vitales para el trabajo con operaciones de fracciones en sexto año:
- Expresar una fracción impropia en notación mixta y viceversa (MEP, 2012, p.183)
- Identificar fracciones homogéneas y heterogéneas (MEP, 2012, p.183)
- Comparar fracciones utilizando los símbolos <, > o = (MEP, 2012, p.183)
Todas estas habilidades son fundamentales para poder desarrollar en octavo año otras habilidades específicas relacionadas al concepto de número racional.
La introducción de los números Racionales en octavo año se debe hacer a partir de lo trabajado con los números fraccionarios positivos en la Educación Primaria, donde los estudiantes adquirieron habilidades relacionadas con las interpretaciones de las fracciones, uso de diferentes representaciones, conocen los procesos de amplificación y simplificación, comparación de fracciones y fracciones equivalentes. Además, están en capacidad de resolver problemas contextualizados que involucren la multiplicación, división, suma y resta de fracciones. Introducir los racionales negativos no es más que una ampliación de los conocimientos ya trabajados. Puede consultar en detalle en la sección Docentes Secundaria.
Uso en la mediación
El problema ¿Cuánto comprar? debe ser utilizado en la I Etapa: Aprendizaje del conocimiento, este proporciona un contexto ideal para conceptualizar los procedimientos de cálculo de las operaciones con fracciones. La situación planteada en el problema, permite un acercamiento empírico, utilizando diferentes representaciones de las fracciones, que coloca las bases para algunos procesos algorítmicos.
Se sugiere para el trabajo estudiantil independiente, la utilización de subgrupos pequeños (dos o tres estudiantes), con el fin de fortalecer la construcción de ideas. La discusión interactiva y comunicativa, es el momento de exponer los procedimientos utilizados en cada subgrupo, así como las dificultades que se han tenido y la forma de superarlas, el docente debe estar atento en este momento ya que las ideas aquí expuestas le permitirán realizar un adecuado cierre. Una posible estrategia es asignar un ingrediente diferente a al menos dos subgrupos, de esta manera se resuelve el problema completo y se discuten dos estrategias para una misma operación. La exposición común de los distintos procedimientos, unos más elaborados que otros, contribuye en el camino de la generalización. La conexión entre el primer contacto intuitivo con las operaciones y el establecimiento de los algoritmos, depende en gran medida de la mediación pedagógica, aprovechar lo expresado por los estudiantes en la discusión para la posterior clausura o cierre.
Para la segunda etapa de la clase: movilización y aplicación de los conocimientos, se sugiere la utilización de contextos reales, que integren con otras áreas (medidas, geometría, estadística y probabilidad). Se deben evitar la realización de grandes lista de ejercicios en prácticas exclusivamente abstractas de operaciones, que calan poco en el aprendizaje de los estudiantes.
Sobre el problema y elementos relevantes del tema
El problema ¿Cuánto comprar? conecta con el área de geometría (áreas) y medidas (litro, kilogramo, tazas). Al igual que este problema se sugiere colocar problemas contextualizados, que permitan un acercamiento natural con las diferentes interpretaciones de la fracción y sus operaciones. La introducción temprana del cálculo algorítmico puede provocar confusiones en su manejo.
El conocimiento de las operaciones con números naturales ejerce una fuerte influencia en el aprendizaje de las operaciones con fracciones. Los estudiantes al tener asimilados los algoritmos con números naturales a menudo tratan de forzar los algoritmos con fracciones de manera que el resultado se ajuste a lo que le dicta su intuición. Por ejemplo, el producto de dos fracciones puede ser menor que cualquiera de ellas, al contrario de lo que sucede en los números naturales.
Otro ejemplo es a la hora de sumar o restar, aplican los operadores sobre los numeradores entre sí y los denominadores entre sí porque generalizan las propiedades de la adición de números naturales en el campo de los números racionales. Se puede pensar de manera errónea que:
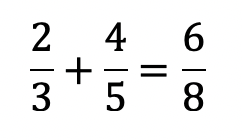
o también que
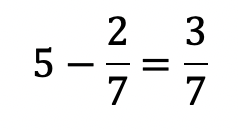
La compresión de las operaciones requiere un adecuado manejo de las diferentes interpretaciones de la fracción, el concepto de fracciones equivalentes y la comparación de fracciones. También los estudiantes deben manejar con fluidez los procesos de amplificación y simplificación.
Para la multiplicación, en el currículo se sugiere trabajar en primera instancia con situaciones contextualizadas que involucren la multiplicación de fracción por natural y de natural por fracción. Luego se debe avanzar al caso general de fracción por fracción, para ello se sugiere trabajar con el modelo de área (MEP, 2012, p.197) intentando ser una ampliación del producto de números naturales. Por último, se debe formalizar el algoritmo para multiplicar.
Para la operación de división, se sugiere trabajar primero la división de un número natural por una fracción, realizando una aproximación gráfica. Luego se abordará dividir una fracción por una fracción, para ello se sugiere utilizar el algoritmo que se apoya en el concepto de fracción inversa, entendida como aquella que restaura a la unidad de una fracción dada (MEP, 2012, p.198)
Para trabajar la suma o resta de forma algorítmica se trabajará sin utilizar el concepto de Mínimo Común Múltiplo (este concepto se aborda hasta sétimo año), por lo que se recomienda para introducir la suma o resta de fracciones, hacerlo gráficamente. Para fracciones heterogéneas, después se precisa el algoritmo para la homogenización de las fracciones por medio de la amplificación o simplificación de fracciones (MEP, 2012, p.199). Por ejemplo:
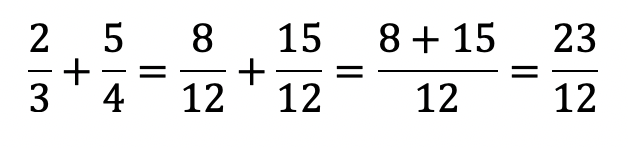
Nivel de complejidad y procesos matemáticos
El nivel de complejidad del problema ¿Cuánto comprar? es de Conexión, esto se asocia con la solución presentada y la intervención de los procesos matemáticos que se describen a continuación:
Razonar y Argumentar:
En el problema se debe responder a una pregunta que no es directa, ¿Cuánta mantequilla, leche y azúcar se necesita para elaborar la receta? Se debe argumentar qué operaciones se deben usar, realizar los cálculos respectivos y luego definir las cantidades que se deben comprar en el supermercado. Lo anterior exige un pensamiento complejo y no algorítmico (no existe una aproximación a la realización de las operaciones bien definida de antemano que pueda recordarse). El proceso está presente en un nivel intermedio.
Plantear y Resolver Problemas:
Para resolver el problema se debe plantear una estrategia no estudiada, pero donde los pasos a seguir se identifican con claridad. Por esta razón este proceso interviene de forma intermedia.
Conectar:
Tiene un grado intermedio de intervención, en la solución se debe conectar algunos conocimientos de la misma área de números (interpretación de una fracción, utilizar diferentes representaciones, amplificar y simplificar) y de otra área, medidas (diversas medidas: masa, capacidad) para resolver un problema de contexto real.
Comunicar:
En la solución es necesario interpretar una secuencia de razonamientos matemáticos y establecer conclusiones mediante lenguaje natural de los resultados en la solución del problema. Por ejemplo, el razonar que 14 ¾ tazas de leche, corresponde a 4 cajas de un litro de leche.
Representar:
En la solución es necesario pasar de la representación numérica(notación fraccionaria o mixta) a la representación gráfica. El proceso está presente en un nivel intermedio.
Por tanto, el nivel de complejidad del problema es de Conexión, debido a las exigencias cognitivas que implica para el estudiante y que fueron detalladas previamente. Se puede profundizar en la estrategia para determinar los niveles de complejidad en Ruiz (2018). Además puede acceder a los videos de la colección Valoración de Tareas Matemáticas para ampliar los contenidos.